转动的黑洞可以发电
在史瓦西度规和RN度规中,g=0的位置恰好也是g→∞的位置,于是这个位置就顺理成章地被定义为黑洞的视界 。可是在克尔度规中,满足这两个条件的位置不再重合 。
解g=0这个方程得到
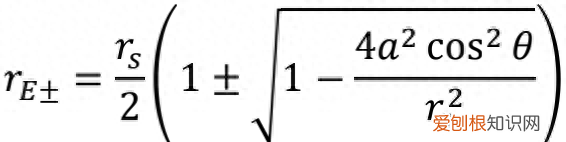
文章插图
解这个方程得到
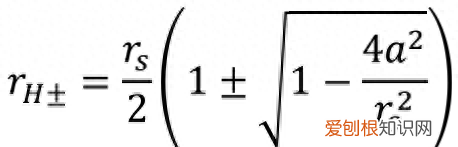
文章插图
这两组解对应四个界面,应该把哪些定义成视界呢?

文章插图
回忆前面对冒险者旅程的描述,我们可以总结出两条结论:
- 当冒险者悬停在空间某一位置时,他的时间流逝速度在远处观者看来正比于,当g=0时,远处观者所看到的冒险者就彻底静止了 。
- 在g<0的地方,空间维r变成了像时间维t一样的单向维度,冒险者无法悬停在空间一点,必须沿r方向持续单向运动 。
这两条对所有时空都是普适的,也可以用来考察克尔度规 。
如果让冒险者前往一个克尔黑洞,当他到达r位置的时候,在远处的我们看来,他就已经静止了,但其实他自己还能继续向前,而且即使进入了r<r的区域,理论上仍然存在逃离的可能性 。只有他进入r<r的区域后,才真正被黑洞捕获,被不可逆转的拖向r位置 。
所以r才是黑洞的事件视界,而r的位置被命名为静止面,也叫无限红移面,在这个位置以降的地方所发出的光,都无法将能量携带到远方 。细心的读者也许会问,连光都无法逃离的地方,冒险者又如何能逃离呢?这就跟r至r之间这片区域的特殊几何特性有关了 。
在这个区域,g>0且g>0,似乎时间维和r维度都变成了“空间维度”,为了让冒险者拥有实数的时间τ,必须在线元表达式里找到一个负数的贡献 。
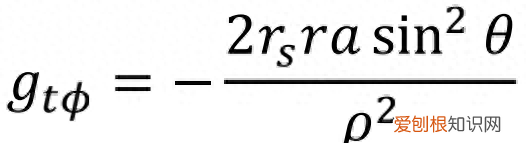
文章插图
就成了唯一可指望的贡献来源 。可见,在r至r间的区域内,是一个无法停止永远单向变化的维度 。这就是自转的黑洞对周围的空间所产生的极端拖拽效应 。
这片时刻转动着的时空被称为能层,因为其中蕴含着一种特殊的能量,进入这个区域的的冒险者可以逆着转动方向抛出一个有质量的物体,自己就可以获得许多能量,继而利用这些能量来逃离出静止面 。这个丢车保帅获取能量的做法叫作“彭罗斯过程”(Penrose process),是彭罗斯在1969年发现的 。
我们知道质量就是能量的一种形式,而彭罗斯过程本质上就是利用克尔黑洞的能层将质量兑换成能量的方法 。而且这种能量兑换方式的效率非常高,我们投喂给黑洞的质量中,理论上最多可以有29%转化为我们获取的能量 。别看这个效率大概跟用煤烧开水的效率差不多,但别忘了我们的分母不是煤炭中的化学能,而是整坨物质的质量 。
事件视界的形状
带有自转角动量J和电荷Q的克尔-纽曼度规是克尔度规的一个小小扩展 。
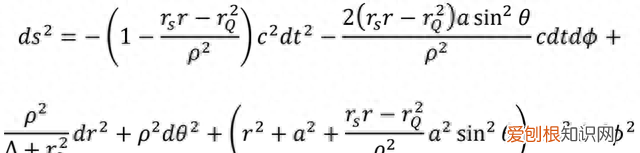
文章插图
可以看出这个度规与克尔度规所描述的时空结构基本没有太多差别,我们同样可以通过g=0和这两个方程找到静止面和事件视界的位置 。

文章插图
和
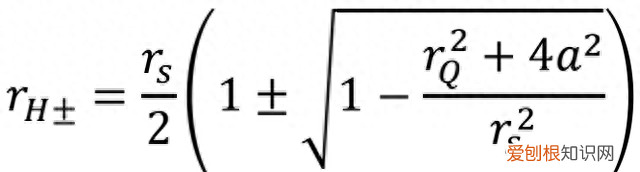
推荐阅读
- 离婚两个孩子的抚养权怎么争取
- 类似铳皇无尽的法夫纳的动漫
- 青铜器本来的颜色是绿色吗为什么
- 口罩戴反了会有影响吗
- 2021年高考出分到填志愿有几天
- 什么是abo设定
- 文件夹如何取消分组,关于电脑的文件夹显示分组问题
- 绝地求生怎么打字
- dnf公会满属性是多少,dnf公会属性只加120吗


