
文章插图
所谓求解广义相对论方程,其实就是计算出度规的所有分量 。对时空几何性质的所有刻画,都藏在这个矩阵里 。
知道了这些,我们就可以根据一个线元的表达式,来阅读出时空度规,继而揣度时空的样子 。比如,把不自转,不带电,质量为M的物体放在极坐标原点,它周围的真空线元表达式是
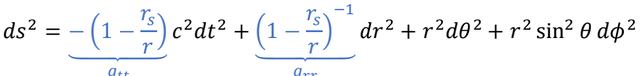
文章插图
其中
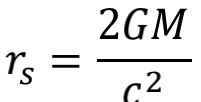
文章插图
我们能马上看出来,这个史瓦西度规仍然是对角矩阵,但是对比平直时空的样子,标成蓝色的g和g两个分量显然有所不同,这两项就是所有后相对论时代对黑洞研究的起点,r就是史瓦西半径,r=r处就是史瓦西黑洞的视界 。
当s→∞的时候,史瓦西度规回到了平直时空的样子,说明在无穷远处时空弯曲的效应逐渐消失 。那么在黑洞附近的时空又是如何弯曲的呢?让我们派出一位冒险者到临近视界的地方进行考察 。三维空间中,冒险者所处的位置是一个点,而四维时空中,由于时间的不断流逝,即使冒险者静止不动这个位置仍是一条线,被称为“世界线” 。
黑洞附近的时间膨胀
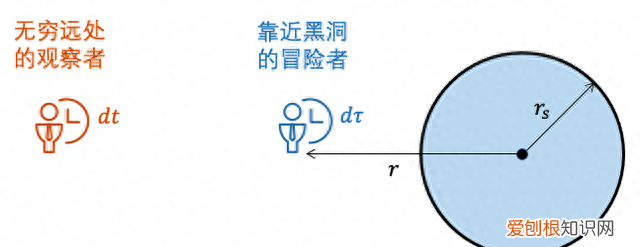
相对论告诉我们,世界线是个绝对的物理对象,无论从哪个参照系中计算,这条线上的同一段ds的长度都必然相同 。我们选取两个特殊的参照系,一个是相对黑洞静止的参照系,另一个是冒险者自己的随动参照系 。
前一个参照系中,我们照旧使用已经提到过的公式来计算冒险者世界线的线元 。

文章插图
其中,代表沿球面切向位置变化,连同径向位置变化dr一起,给出冒险者的空间坐标位置变化 。需要注意的是式子中的dt,它代表站在无穷远处且相对黑洞静止的观者所感受到的时间变化 。
在后一个参照系中,冒险者自己相对于随动参照系没有任何位置变化,只是单纯地经历着时间的流逝,所以线元就简化成了
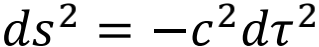
文章插图
其中dτ就是冒险者自己所感受到的时间变化 。
文章插图
两个参照系中冒险者的世界线是同一根,所以
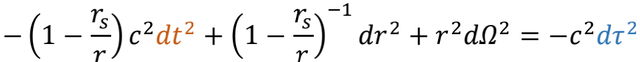
文章插图
现在,我们命令冒险者悬停,于是dr和dΩ都是0,式子就简化成了
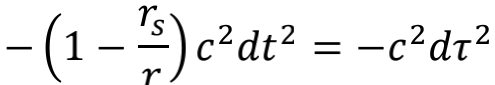
文章插图
如果悬停的位置满足r=1.01r,就会有dt≈10dτ,冒险者的时钟变得好慢!无穷远处的观者不得不等上十年,才能看到冒险者长了一岁,这就是引力场所产生的时间膨胀效应 。如果冒险者此时向远处发射一道光,那么等光到达远处的观者时频率已经下降为出发时的十分之一,也就是产生了严重的红移 。
当冒险者的位置无限接近r时,时间膨胀也无限接近无穷大 。尽管冒险者自己仍然体验着正常的时间流逝,但在远处的观者看来,冒险者的时间已近乎停止,其发出的光,频率也无限接近零 。也就是说,源自视界处的光,无法将能量传递到远方 。忽然想到有那么多电视节目甚至电台都乐意取“视界”做名字,不免让人感觉……
推荐阅读
- 离婚两个孩子的抚养权怎么争取
- 类似铳皇无尽的法夫纳的动漫
- 青铜器本来的颜色是绿色吗为什么
- 口罩戴反了会有影响吗
- 2021年高考出分到填志愿有几天
- 什么是abo设定
- 文件夹如何取消分组,关于电脑的文件夹显示分组问题
- 绝地求生怎么打字
- dnf公会满属性是多少,dnf公会属性只加120吗


