爱刨根知识网

  1. 首页 > 经验知识 > >

近似算法有哪些,举例说明什么是最优算法

生活经验算法

罗素曾说：所有精确科学都被近似思想所主宰 。本文介绍了近似算法及其对某些标准问题的适用性 。
新冠大流行给世界带来了巨大的改变，全球科学家和研究人员在研制有效的疫苗 。他们正在做的就是从广阔的样本空间中近似地收紧可能性范围，并尽力得到一些有效解 。近似在我们的生活中发挥了重要作用 。
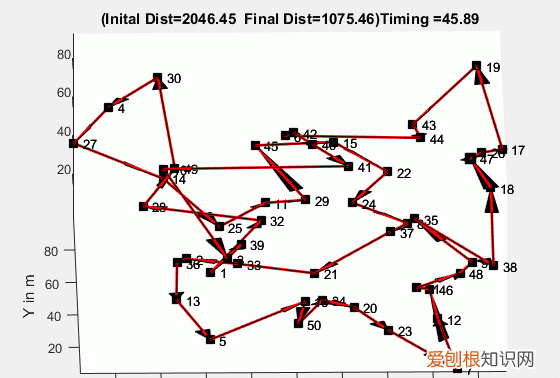
以在线食品配送为例，我们经常从网上订购食物，享受快速送达的服务 。但你想过这些 app 后端运行的什么算法让快递员在更短时间内抵达目的地吗？答案是近似算法 。这类问题就是「旅行商问题」 。
近似算法有哪些,举例说明什么是最优算法

文章插图
食品配送：旅行商问题的现实应用 。
本文将介绍近似算法及其对某些标准问题的适用性，以及哪些因素会影响到特定算法的选择 。
什么是近似算法？
近似算法是一种处理优化问题 NP 完全性的方式，它无法确保最优解 。近似算法的目标是在多项式时间内尽可能地接近最优值 。
它虽然无法给出精确最优解，但可以将问题收敛到最终解的近似值 。其目标满足以下三个关键特性：
能够在多项式时间内高效运行；
能够给出最优解；
对于每个问题实例均有效 。
背景
数学表达式的评估常伴随常量、变量分析和方程的阶，可用于衡量近似的复杂度 。此类评估将问题分解为 P 和 NP 难问题 。
P 问题和 NP 问题的策略
P 问题是指可以在多项式时间内求解的问题 。
NP 表示不确定性多项式时间（nondeterministic polynomial time），NP 问题是指在多项式时间内近似验证答案的问题 。但目前人们发现，很多此类问题需要指数时间才能求解 。
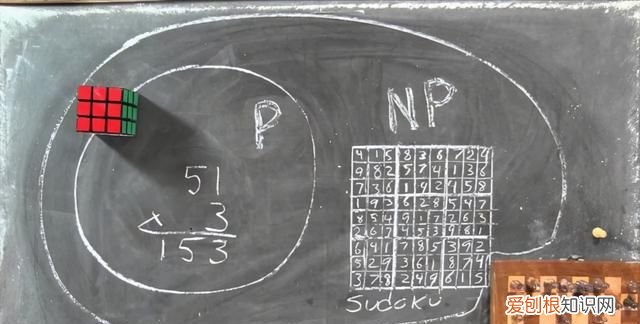
近似算法有哪些,举例说明什么是最优算法

文章插图
P 和 NP 策略 。
真正的争论在于 P=NP 还是 P≠NP 。之前的一些研究证明这两种都是对的 。如果一个问题是多项式次方，则存在多个最优算法 。因此，在 NP 完全问题中，存在两种方法找到近优解，然后选择最适合的算法 。
如果输入的大小比较小，则具备指数运行时间的算法可能会比较适合 。
其次，通过用近似算法替代确定性算法，我们仍然能够在多项式时间内找到近优解 。
近似算法的复杂度可以从输入大小和近似因子中推断出来 。接下来，我们通过一些示例，深入探索这些算法如何应用到现实问题中 。
分区问题（Partition Problem）
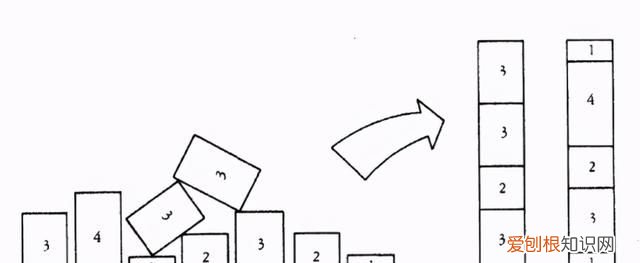
在计算机科学领域，该问题的定义是：给定多重正整数集 X，它可以被分割为两个元素之和相等的子集 X1 和 X2，即每个子集的数值之和与另一个子集相等 。
近似算法有哪些,举例说明什么是最优算法

文章插图
例如，X={3,4,1,3,3,2,3,2,1} 可以被分割为 X1={3,3,2,3} 和 X2={4,2,3,1,1}，二者的数值之和都是 11 。
类似地，X={1,3,1,2,1,2} 可以被分成 X1={2,1,1,1} 和 X2={3,2}，两个子集的数值之和都是 5 。有趣的是，这不是唯一解 。X1={1,3,1} 和 X2={2,1,2} 的数值之和也为 5，这表明存在多个可能的子集 。
这就是 NP 完全问题，存在伪多项式时间动态规划解，可获得该问题的近优解 。
方法和决定步骤
现在，我们开始分析这个问题，把它分解成数个单独的标准问题 。这里，我们想要找出多重集的元素之和相等的子集，那么该问题就可以分解成以下两个问题：
子集和问题：子集 X 的元素之和等于数字 W 。
多路数字分割：给定整数参数 W，确定如何将 X 分割成 W 个等额子集 。
近似算法
如上所述，将分区问题分解为多路分割与子集和问题后，我们就可以考虑为这些问题而开发的算法，包括：

推荐阅读


上一篇：缸内积碳有必要清洗，发动机积碳需要清理吗

下一篇：一山望着一山高的意思