爱刨根知识网

  1. 首页 > 经验知识 > >

近似算法有哪些,举例说明什么是最优算法( 二 )

生活经验算法


贪婪数字分割（Greedy number Partitioning）
该算法循环遍历所有数字，将每个数字分配给总和最小的子集 。如果数字未以排序方式排列，则其运行时复杂度为 O(n)，近似率约为 3/2 。其 Python 伪代码如下：
def find_partition(numbers): """Separate the available numbers into two eqal sum series.
Args: numbers: collection of numbers, for example list of integers.
Returns: Two lists of numbers. """ X = [] Y = [] sum_X = 0 sum_Y = 0 for n in sorted(numbers, reverse=True): if sum_X < sum_Y: X.append(n) sum_X = sum_X + n else: Y.append(n) sum_Y = sum_Y + n return (X, Y)
将数字排序，则运行时复杂度增加到 O(n logn)，近似率增加到 7/6 。如果数字在 [0,1] 范围内均匀分布，则近似率约为 1 + O(log logn/n) 。

近似算法有哪些,举例说明什么是最优算法

文章插图
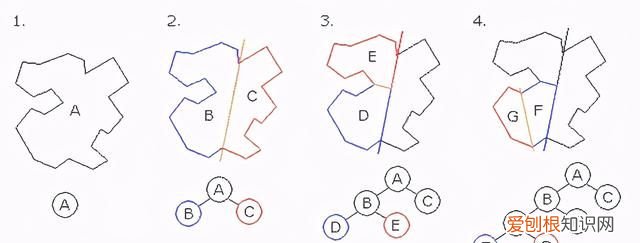
分区问题图示 。
上图用二叉树的形式展示所有分区 。树的根部表示集合中的最大数，每一级对应输入数字，每个独立分支对应不同的子集 。遍历这些集合需要深度优先遍历（depth-first traversal），所需的空间复杂度为 O(n)，时间复杂度为 O(2^n) 。
适用性：
该算法可以根据情况进行修改，以便改善运行时复杂度 。每一级的首要目标是构建一个分支，将当前数字分配给总和最小的子集 。首先通过贪婪数字分割找出总和，然后切换到优化，得到全多项式时间近似解 。
Karmarkar-Karp 算法
Karmarkar-Karp 算法指以降序方式排列数字的最大差分方法，该方法将差值替换掉原来的数字不断放进集合中 。其 Java 伪代码实现如下：
int karmarkarKarpPartition(int[] baseArr) { // create max heap PriorityQueue heap = new PriorityQueue(baseArr.length, REVERSE_INT_CMP);
for (int value : baseArr) { heap.add(value); }
while (heap.size() > 1) { int val1 = heap.poll(); int val2 = heap.poll(); heap.add(val1 - val2); }
return heap.poll();}
该算法包含输入集 S 和参数 k 。将 S 分割成 k 个子集，使这些子集中的数字总和相等，从而构建期望输出 。该算法包含如下关键步骤：
以降序方式排列数字；
用差值替换掉原来的数字，直到只有一个数字；
采用回溯算法，完成分区 。
适用性：
该算法通过构建二叉树来假设分区 。每一级表示一对数字，左侧的分支表示用差值替换数字，右侧的分支表示将差值放置在同一个子集中 。该算法先通过最大差分求得解，然后继续寻找更好的近似解 。它所需的空间复杂度为 O(n)，但最糟糕的情况下所需的时间复杂度可能会达到 O(2^n) 。
装箱问题
装箱问题有多种现实应用 。例如，如何从根本上改善印度的垃圾管理系统 。这个问题就可以通过装箱问题来解决，帮助当局决定 x 量的垃圾需要多少个垃圾箱 。
近似算法有哪些,举例说明什么是最优算法

文章插图
集装箱船：装箱问题的现实应用 。
在计算机科学领域中，该问题可用于多种内存管理技术 。在该算法中，我们可以通过去除冗余和最小化空间浪费来包装不同形状和大小的对象 。
例如：给定一个包含 n 个项的集合，每个项的大小分别为 s1,s2,..,sn (0
经典方法：
1. 邻近适应算法 (Next Fit)：查看当前项是否适合当前箱子 。如果适合，则将物品放置在箱子里，否则开启一个新的箱子 。
我们来看一个示例：项是 0.5, 0.7, 0.5, 0.2, 0.4, 0.2, 0.5, 0.1, 0.6，箱子大小均为 1 。
近似算法有哪些,举例说明什么是最优算法

文章插图
基于邻近适应算法的装箱解决方案（M = 箱子总数 = 6） 。
2. 最先匹配法 (First Fit)：按顺序浏览箱子，在第一个箱中放置新的项，直到放不下再启用新的箱子 。

推荐阅读


上一篇：缸内积碳有必要清洗，发动机积碳需要清理吗

下一篇：一山望着一山高的意思