椭圆中abc的关系
椭圆中abc的关系:a2=b2+c2(a>b>0) 。长轴是2a,短轴是2b,焦距是2c 。椭圆是平面内到定点F1、F2的距离之和等于常数(大于|F1F2|)的动点P的轨迹,F1、F2称为椭圆的两个焦点 。其数学表达式为:|PF1|+|PF2|=2a(2a>|F1F2|) 。
椭圆的参数方程:x=acosθ,y=bsinθ 。求解椭圆上点到定点或到定直线距离的最值时,用参数坐标可将问题转化为三角函数问题求解 。x=a×cosβ,y=b×sinβ,a为长轴长的一半,b为短轴长的一半 。设F1、F2为椭圆C的两个焦点,P为C上任意一点 。若直线AB为C在P点的法线,则AB平分∠F1PF2 。
椭圆中abc等量关系是什么椭圆中abc等量关系为a2=b2+c2(a>b>0) 。
椭圆的abc是什么意思椭圆的a表示长轴距离,b表示短轴距离,c表示焦距 。
椭圆是shis平面内到定点F1、F2的距离之和等于常数(大于|F1F2|)的动点P的轨迹,F1、F2称为椭圆的两个焦点 。其数学表为:|PF1|+|PF2|=2a(2a>|F1F2|) 。椭圆是圆锥曲线的一种,即圆锥与平面的截线 。椭圆的周长等于特定的正弦曲线在一个周期内的长度 。
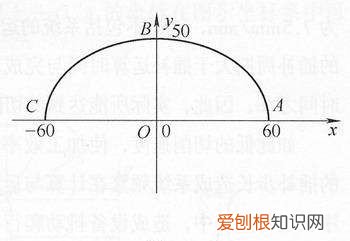
文章插图
扩展资料:
椭圆是封闭式圆锥截面:由锥体与平面相交的平面曲线 。椭圆与其他两种形式的圆锥截面有很多相似之处:抛物面和双曲线,两者都是开放的和无界的 。圆柱体的横截面为椭圆形,除非该截面平行于圆柱体的轴线 。
椭圆也可以被定义为一组点,使得曲线上的每个点的距离与给定点(称为焦点或焦点)的距离与曲线上的相同点的距离的比值给定行(称为directrix)是一个常数 。该比率称为椭圆的偏心率 。
在平面直角坐标系中,用方程描述了椭圆,椭圆的标准方程中的“标准”指的是中心在原点,对称轴为坐标轴 。
椭圆的标准方程有两种,取决于焦点所在的坐标轴:
1)焦点在X轴时,标准方程为:
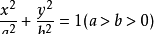
文章插图
2)焦点在Y轴时,标准方程为:
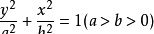
文章插图
椭圆上任意一点到F1,F2距离的和为2a,F1,F2之间的距离为2c 。而公式中的b2=a2-c2 。b是为了书写方便设定的参数 。
又及:如果中心在原点,但焦点的位置不明确在X轴或Y轴时,方程可设为mx2+ny2=1(m>0,n>0,m≠n) 。即标准方程的统一形式 。
椭圆的面积是πab 。椭圆可以看作圆在某方向上的拉伸,它的参数方程是:x=acosθ , y=bsinθ
标准形式的椭圆在(x0,y0)点的切线就是 :xx0/a2+yy0/b2=1 。椭圆切线的斜率是:-b2x0/a2y0,这个可以通过复杂的代数计算得到 。
参考资料:
椭圆里abc的关系公式椭圆里abc的关系可表示为:a2=b2+c2 。
椭圆的a表示长轴距离,b表示短轴距离,c表示焦距 。
长轴长:2a;短轴长;2b;焦点距离:2c;离心率:c/a 。
椭圆与圆很相似 。不同之处在于椭圆有不同的x和y半径,而圆的x和y半径是相同的 。在数学中,椭圆是平面上到两个固定点的距离之和是同一个常数的点的轨迹 。这两个固定点叫做焦点 。它是圆锥曲线的一种,即圆锥与平面的截线 。椭圆在方程上可以写为标准式x2/a2+y2/b2=1 。
几何性质:
1、范围:焦点在x轴上-a≤x≤a-b≤y≤b;焦点在y轴上-b≤x≤b-a≤y≤a 。
2、对称性:关于X轴对称,Y轴对称,关于原点中心对称 。
3、顶点:(a,0),(-a,0),(0,b),(0,-b) 。
4、离心率:e=c/a 。
5、离心率范围0
椭圆中abc的关系式是什么椭圆截与两焦点连线重合的直线所得的弦为长轴,长为2a 。
推荐阅读
- 怎么区分高铁和动车,动车和高铁有什么区别
- 用电子身份证可以坐高铁吗 身份证掉了怎么坐动车高铁
- 南方暴雨今天达到高峰 有人逆行撑起“安全伞”
- 前是什么时期,中华民族5千年的历史描写
- 循环经济的五种商业模式 五种商业模式
- 舍身为己什么意思,舍己为人什么意思
- 五种疾病不能接种新冠肺炎疫苗
- 如何清洗菜花,如何把大块菜花切成小块
- 如何做酸辣鸡爪,教你怎么做酸辣鸡脚


