代数余子式和余子式的区别
代数余子式和余子式的区别在于:
1、指代不同
余子式:行列式的阶越低越容易计算,于是很自然地提出,能否把高阶行列式转换为低阶行列式来计算 。
代数余子式:在n阶行列式中,把元素a??i所在的第o行和第e列划去后,留下来的n-1阶行列式叫做元素a??i的余子式 。
2、特点不同
余子式:关于一个k阶子式的余子式,是A去掉了这个k阶子式所在的行与列之后得到的(n-k)×(n-k)矩阵的行列式 。
代数余子式:元素a??i的代数余子式与该元素本身没什么关系,只与该元素的位置有关 。
3、用处不同
余子式:转置矩阵称为A的伴随矩阵,伴随矩阵类似于逆矩阵,并且当A可逆时可以用来计算它的逆矩阵 。
代数余子式:计算元素的代数余子式时,首先要注意不要漏掉代数余子式所带的代数符号 。计算某一行(或列)的元素代数余子式的线性组合的值时,尽管直接求出每个代数余子式的值,再求和也是可行的 。
余子式和代数余子式是什么意思代数余子式是从行列式的公式中提取出来的,它的作用是把n阶行列式化简为n – 1阶行列式 。在n阶行列式中,把元素a??i所在的第o行和第e列划去后,留下来的n-1阶行列式叫做元素a??i的余子式,记作M??,将余子式M??再乘以-1的o+e次幂记为A??,A??叫做元素a??的代数余子式 。
在n阶行列式中,划去元aij所在的第i行与第j列的元,剩下的元不改变原来的顺序所构成的n-1阶行列式称为元aij的余子式 。
关系:
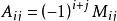
文章插图
代数余子式本身是n - 1阶行列式,它可以继续展开成n - 2阶行列式……如此展开下去,直到1阶行列式为止,其核心思想是把一个复杂的高阶行列式转换成多个简单的低阶行列式 。
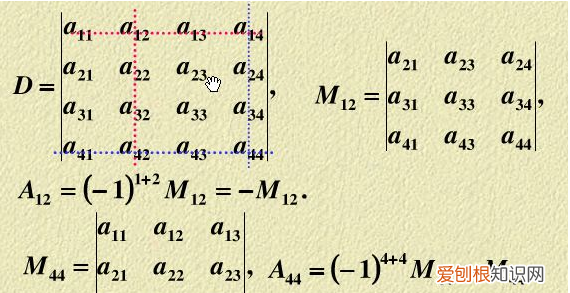
文章插图
扩展资料
代数余子式本身就是行列式,只是它的正负号需要单独判断,判断方法是根据选定元素行号和列号之和的奇偶性 。用Cij表示aij的代数余子式,当i + j是偶数时,行列式取正号,是奇数则取符号 。比如三阶行列式中,C12的行列号之和是3,它对应的代数余子式取符号 。
通过消元法计算是正确的选择,通常也应该这么做,实际上不难看出这个A是一个奇异矩阵,所以它的行列式等于0,现在用行列式的公式来验证这个结论 。根据公式,|A|的大多数展开项都等0,没有被淘汰的只有两项,二者相加等于0:
余子式和代数余子式有什么区别和联系一、指代不同
1、余子式:行列式的阶越低越容易计算,于是很自然地提出,能否把高阶行列式转换为低阶行列式来计算 。
2、代数余子式:在n阶行列式中,把元素a??i所在的第o行和第e列划去后,留下来的n-1阶行列式叫做元素a??i的余子式
二、特点不同
1、余子式:关于一个k阶子式的余子式,是A去掉了这个k阶子式所在的行与列之后得到的(n-k)×(n-k)矩阵的行列式 。
2、代数余子式:元素a??i的代数余子式与该元素本身没什么关系,只与该元素的位置有关 。
三、用处不同
1、余子式:转置矩阵称为A的伴随矩阵,伴随矩阵类似于逆矩阵,并且当A可逆时可以用来计算它的逆矩阵 。
2、代数余子式:计算元素的代数余子式时,首先要注意不要漏掉代数余子式所带的代数符号。计算某一行(或列)的元素代数余子式的线性组合的值时,尽管直接求出每个代数余子式的值,再求和也是可行的 。
代数余子式和余子式的关系在n阶行列式中,吧(i,j)元aij所在的第i行和第j列划去后,留下来的n-1阶行列式叫做(i,j)元aij的余子式,记做Mij;记Aij=[(-1)^(i+j)]*Mij,Aij叫做(i.j)元的代数余子式 。
例如在四阶行列式中(3,2)元的a32的余子式和代数余子式分别为A32=[(-1)^(3+2)]*M32=-M32
(其中aij
Aij
Mij
A32中的ij和32都是对应的角标)
余子式和代数余子式有什么区别和联系余子式和代数余子式有三个区别:指代不同、特点不同、用处不同 。
一、指代不同
1、余子式:行列式的阶数越低,越容易计算 。因此,我们自然会问一个高阶行列式能否转换成低阶行列式进行计算 。
2、代数余子式:在第n阶行列式中,去掉元素a的另一行和e列??I后,剩下的n-1阶行列式称为元素a-I的余子式
二、特点不同
1、余子式:关于一个k阶子式的余子式,是A去掉了这个k阶子式所在的行与列之后得到的(n-k)×(n-k)矩阵的行列式 。
2、代数余子式:元素a??i的代数余子式与该元素本身没什么关系,只与该元素的位置有关 。

文章插图
三、用处不同
1、余子式:转置矩阵称为A的伴随矩阵 。伴随矩阵类似于逆矩阵,当A可逆时可用来计算A的逆矩阵 。
2、代数余子式:在计算元素的代数余子式时,首先要注意不要忽略余子式的代数符号 。当计算一行(或一列)的元素余因子的线性组合时,可以直接计算每个余因子,然后将其求和 。
【代数余子式和余子式的区别,余子式和代数余子式是什么意思】以上就是关于代数余子式和余子式的区别,余子式和代数余子式是什么意思的全部内容,以及代数余子式和余子式的区别的相关内容,希望能够帮到您 。
推荐阅读
- 工作中异性缘非常好的四大星座男
- 蚌精的盾怎么算
- 怎么搜索陌生微信群
- 什么是审判机关
- 蔚来总部在哪
- 猫砂有没有保质期
- paperok查重会被盗用吗
- 预售合同签完还签正式合同吗
- 沙棘的功效与作用 沙棘是什么


