如何找间断点，怎样判断是不是可去间断点

如何找间断点
函数间断点寻找的方法：无定义的点，就是间断点。在非连续函数y=f(x)中某点处，xo处有中断现象，那么，xo就称为函数的不连续点，即间断点。
如果函数f(x)有下列情形之一：
1、函数f(x)在点x0的左右极限都存在但不相等，即f(x0+)≠f(x0-)；
2、函数f(x)在点x0的左右极限中至少有一个不存在；
3、函数f(x)在点x0的左右极限都存在且相等，但不等于f(x0)或者f(x)在点x0无定义。
则函数f(x)在点x0为不连续，而点x0称为函数f(x)的间断点。
怎样判断是不是可去间断点若f(x)函数在点X0处不连续，则称点X0为函数f(x)的不连续点或间断点，函数间断点的分类如下：
第一类间断点：函数f（x）在X0处的左极限和右极限都存在
。第一类间断点包含以下两类：
（1）可去间断点：函数f（x）在X0处的左极限等于右极限；
（2）跳跃间断点：函数f（x）在X0处的左极限不等于右极限；
第二类间断点：函数f（x）在X0处的左极限和右极限至少有一个不存在。
方法总结：判断函数间断点的类型，关键在于看函数在间断点处的左右极限是否存在。
方法总结：判断函数间断点的类型，关键在于看函数在间断点处的左右极限是否存在。

文章插图
如何判断一元函数可导一、第一类间断点：左右极限存在。
当左右极限相等，则称为可去间断点；左右极限不等，则称为跳跃间断点。
设Xo是函数f(x)的间断点，那么如果f(x-)与f(x+)都存在，则称Xo为f(x)的第一类间断点。
又如果：
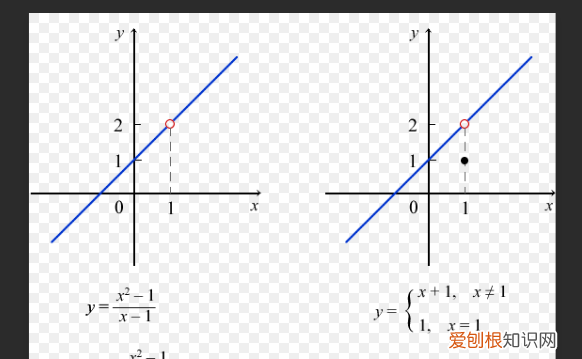
1、f(x-)=f(x+)≠f(x),或f(x)无意义，则称Xo为f(x)的可去间断点。
2、f(x-)≠f(x+),则称Xo为f(x)的跳跃间断点。
二、第二类间断点：左右极限至少有一个不存在。
如果有一个极限趋于无穷大，则称为无穷间断点；否则称为振荡间断点。
第二类间断点是指函数的左右极限至少有一个不存在。第二类间断点有非常多种，如无穷间断点，振荡间断点，单侧间断点，狄利克雷函数间断点等等。
第二类间断点：函数的左右极限至少有一个不存在。
1、若函数在x=Xo处的左右极限至少有一个无穷不存在,则称x=Xo为f(x)的无穷间断点。例y=tanx，x=π/2 。
2、若函数在x=Xo处的左右极限至少有一个振荡不存在，则称x=Xo为f(x)的振荡间断点。例y=sin(1/x),x=0 。

文章插图
扩展资料
函数间断点的判定：
1、求函数的定义域，找出分割定义域为定义区间的分割点与分段函数的分界点xk；
2、对xk求函数的左右极限，由左右极限的存在性及相关的极限值与变化趋势，确定间断点类型。
3、间断点存在的位置为分段函数的分界点，或者函数定义区间的分割点。没有定义的点构成区间则不为函数的间断点，为函数没有定义的区间。
如何判断间断点的类型【如何找间断点，怎样判断是不是可去间断点】判断间断点的技巧：
1、第一类间断点：该点左右极限都存在，可分为：
（1）可去间断点：左右极限相等。
（2）跳跃间断点：左右极限不相等。
2、第二类间断点：左右极限中有一个不存在，可分为：
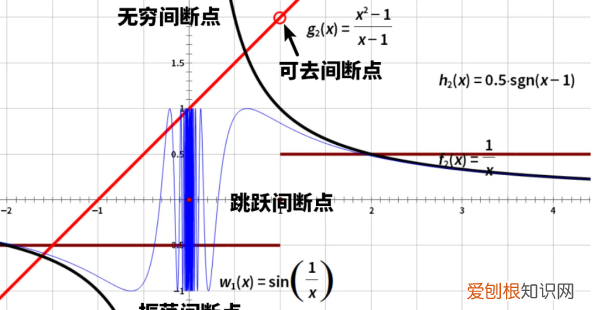
（1）无穷间断点：在间断点的极限为无穷大。
（2）震荡间断点：在间断点的极限不稳定存在。

文章插图
间断点是指：在非连续函数y=f(x)中某点处xo处有中断现象，那么，xo就称为函数的不连续点。

如何找间断点，怎样判断是不是可去间断点

推荐阅读

关于节约粮食的名言诗句关于节约粮食的名言和诗句

奋斗励志朋友圈句子励志短句致自己奋斗朋友圈

想发朋友圈表示心情不好的句子心情不好发朋友圈的句子心情短句

贝拉玻尿酸是合法的吗贝拉玻尿酸是进口的还是国产的

核桃仁做菜的菜谱，您知道桃仁脆溜鸡的做法

浅紫色显皮肤黑还是白

库伦旗景点

居家隔离和集中隔离的区别什么情况下要隔离28天

蝉蛹是什么

怎样能丰胸最安全有效