
文章插图

文章插图
01
分式方程的概念
(1)定义:分母中含有未知数的方程叫分式方程 。(2)分式方程的重要特征:首先必须是等式 , 其次方程里需含有分式 , 即分母不全为1 , 而分母中需含有未知数 。(3)分式方程和整式方程的区别就在于分母中是否有未知数(不是一般的字母系数) , 分母中含有未知数的方程是分式方程 , 分母中不含有未知数的方程是整式方程 。(4)分式方程和整式方程的联系:分式方程可以转化为整式方程 。
02
分式方程的解法
解分式方程的基本思想:将分式方程转化为整式方程 , 转化方法是方程两边都乘以最简公分母 , 去掉分母 。在去分母这一步变形时 , 有时可能产生使最简公分母为零的根 , 这种根叫做原方程的增根 。因为解分式方程时可能产生增根 , 所以解分式方程时必须验根 。
03
解分式方程的一般步骤
(1)方程两边都乘以最简公分母 , 去掉分母 , 化成整式方程(注意:当分母是多项式时 , 先分解因式 , 再找出最简公分母) 。(2)解这个整式方程 , 求出整式方程的解 。
(3)检验:将求得的解代入最简公分母 , 若最简公分母不等于0 , 则这个解是原分式方程的解 , 若最简公分母等于0 , 则这个解不是原分式方程的解 , 原分式方程无解 。
04
重要考点
(1)考点一:分式的基本性质
分式的分子和分母乘(或除以)同一个不等于0的整式 , 分式的值不变 。注意应用分式时 , 体会同的含义 , 避免犯只乘分子或只乘分母的错误 。
例1:如果分式
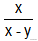
文章插图
中的x和y都扩大为原来的3倍 , 那么分式的值( )
A.不变
B.扩大为原来的3倍
C.扩大为原来的6倍
D.扩大为原来的9倍
【答案】A 。由分式的基本性质可知 , 分母可以提出公因式3 , 相当于原分子分母同时乘以3 , 那么分式的值不变 。
(2)考点二:分式方程定义
分母中含未知数的方程叫做分式方程 。其中使最简公分母为0的根叫做分式方程的整根 。要注意验证根 , 将整式方程的解代入最简公分母 , 如果最简公分母的值不为0 , 则整式方程的解就是原分式方程的解 , 否则 , 这个解不是原分式方程的解 。
例2:求下面方程的解 。
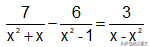
文章插图
【答案】
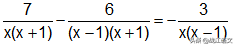
文章插图
【如何去分母】
7(x-1)-6x=-3(x+1)
x=1
经检验x=1时 , x(x-1)(x+1)=0
故x=1不是原分式方程的根 , 舍去
所以原分式方程无解
声明:本文转自初中数学 , 以上图文 , 贵在分享 , 版权归原作者及原出处所有 , 若涉及版权等问题请联系删除 。

文章插图
推荐阅读
- 种植辣椒用什么肥料,种辣椒用什么肥料比较好
- 简笔画爱心怎么画,爱心萌可怎么画简单又好看又可爱
- ios系统其他系统数据占用过大 ios13系统占用空间大
- 如何删除日程计划,怎么取消vivo手机上的HD
- 格桑花的种子需要泡,格桑花种子发芽后什么时候能移植
- 氢氧化钠与氧化铁反应生成什么化学方程式 氧化铁和氢氧化钠
- 如何解决电脑任务管理器没有边框
- 小米6丢失模式怎么解除,小米手机手机卡拔不出来怎么办
- 改照片底色的软件 如何改照片底色


