爱刨根知识网

  1. 首页 > 经验知识 > >

初中数学二次函数知识点梳理！ 初中二次函数

生活经验经验分享

初中二次函数（初中数学二次函数知识点梳理！）
一、定义与定义表达式
一般地，自变量x和因变量y之间存在如下关系：y=ax+bx+c（a，b，c为常数，a≠0，且a决定函数的开口方向，a>0时，开口方向向上，a<0时，开口方向向下，IaI还可以决定开口大小，IaI越大开口就越小，IaI越小开口就越大），则称y为x的二次函数 。
二次函数表达式的右边通常为二次三项式 。
二、二次函数的三种表达式
一般式：y=ax+bx+c（a，b，c为常数，a≠0）
顶点式：y=a(x-h)+k[抛物线的顶点P（h，k）
交点式：y=a(x-x?)(x-x?)[仅限于与x轴有交点A（x?，0）和B（x?，0）的抛物线]
注：在3种形式的互相转化中，有如下关系：
h=-b/2a
k=(4ac-b)/4a
x?,x?=(-b√b-4ac)/2a
【初中数学二次函数知识点梳理！ 初中二次函数】三、二次函数的图像
在平面直角坐标系中作出二次函数y=x^2的图像，可以看出，二次函数的图像是一条抛物线 。
四、抛物线的性质
1.抛物线是轴对称图形 。对称轴为直线x=-b/2a 。
对称轴与抛物线唯一的交点为抛物线的顶点P 。特别地，当b=0时，抛物线的对称轴是y轴（即直线x=0） 。
2.抛物线有一个顶点P，坐标为：P(-b/2网a，(4ac-b)/4a) 。当-b/2a=0时，P在y轴上；当=b-4ac=0时，P在x轴上 。
3.二次项系数a决定抛物线的开口方向和大小 。
当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口 。|a|越大，则抛物线的开口越小 。
4.一次项系数b和二次项系数a共同决定对称轴的位置 。
当a与b同号时（即ab＞0），对称轴在y轴左；当a与b异号时（即ab＜0），对称轴在y轴右 。
5.常数项c决定抛物线与y轴交点 。抛物线与y轴交于（0，c） 。
6.抛物线与x轴交点个数：
=b-4ac＞0时，抛物线与x轴有2个交点 。
=b-4ac=0时，抛物线与x轴有1个交点 。
=b-4ac＜0时，抛物线与x轴没有交点 。X的取值是虚数（x=-b√b－4ac的值的相反数，乘上虚数i，整个式子除以2a）
五、二次函数与一元二次方程网
特别地，二次函数（以下称函数）y=ax+bx+c 。
当y=0时，二次函数为关于x的一元二次方程（以下称方程），即ax+bx+c=0 。
此时，函数图像与x轴有无交点即方程有无实数根 。函数与x轴交点的横坐标即为方程的根 。
1.二次函数y=ax，y=a(x-h)，y=a(x-h)+k，y=ax+bx+c(各式中，a≠0)的图象形状相同，只是位置不同 。
它们的顶点坐标及对称轴如下表：

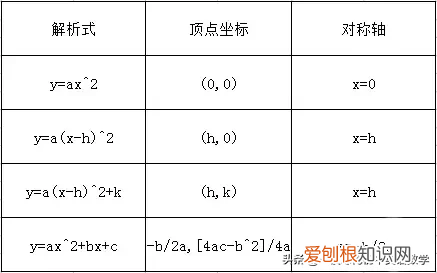
初中数学二次函数知识点梳理！ 初中二次函数

文章插图
当h>0时，y=a(x-h)的图象可由抛物线y=ax向右平行移动h个单位得到 。
当h<0时，则向左平行移动|h|个单位得到 。
当h>0，k>0时，将抛物线y=ax向右平行移动h个单位，再向上移动k个单位，就可以得到y=a(x-h)+k的图象 。
当h>0，k<0时，将抛物线y=ax向右平行移动h个单位，再向下移动|k|个单位可得到y=a(x-h)+k的图象 。
当h<0，k>0时，将抛物线向左平行移动|h|个单位，再向上移动k个单位可得到y=a(x-h)+k的图象 。
当h<0,k<0时，将抛物线向左平行移动|h|个单位，再向下移动|k|个单位可得到y=a(x-h)+k的图象 。
因此，研究抛物线y=ax+bx+c(a≠0)的图象，通过配方，将一般式化为y=a(x-h)+k的形式，可确定其顶点坐标、对称轴，抛物线的大体位置就很清楚了．这给画图象提供了方便．
2.抛物线y=ax+bx+c(a≠0)的图象：当a>0时，开口向上，当a<0时开口向下，对称轴是直线x=-b/2a，顶点坐标是(-b/2a，[4ac-b]/4a)．
3.抛物线y=ax+bx+c(a≠0)，若a>0，当x≤-b/2a时，y随x的增大而减小；当x≥-b/2a时，y随x的增大而增大．若a<0，当x≤-b/2a时，y随x的增大而增大；当x≥-b/2a时，y随x的增大而减小．

推荐阅读


上一篇：面对任何新技术，请先思考这3个问题 | 冷眼读书·未来特辑 ③

下一篇：提香《花神》赏析 提香花神